連立方程式とは？解き方を徹底解説！計算方法から文章題までマスターしよう！【中2数学｜高校入試頻出】
中学生になると習う方程式ですが、中学2年生では連立方程式、中学3年生では二次方程式へと各学年で少しずつレベルアップしていきます。今回は中2で習う連立方程式について解説します。
「1次方程式の解き方はわかったけど連立方程式で計算できない！」
「計算が多くて時間がかかってしまう」
「連立方程式の文章題がどうしても解けない！」
そんなお悩みを持っている人はぜひ最後までご覧ください。
目次
連立方程式とは
1次方程式は基本的に１つの文字に当てはまる数を求めるものですが、連立方程式は、複数の式を使って複数の値を求める方程式です。連立方程式では2つの文字を含んだ2つの式を組み合わせて解く方程式が多く出題されます。
※3つ以上の文字を含んだ連立方程式もありますが、中学数学ではほとんどが2つの文字を含む連立方程式です。
連立方程式が苦手になってしまう原因
連立方程式は2つの式を組み合わせて解くため、1次方程式よりも計算が多く、さらに複雑です。小数や分数が含まれる式もあり、計算が得意でない人は苦手と感じることが多いでしょう。また、式同士を足したり引いたりするので、新しい計算に戸惑うこともあるかもしれませんね。しかし、やり方を覚え、計算の練習を積み重ねれば連立方程式は得点源にもなります。
連立方程式の解き方
連立方程式の解き方には二通りあります。どんな時にどの解き方をするとよいのかを理解して、効率よく計算を進められるようにしましょう。
連立方程式は、2つの文字が含まれているために普通に解くことができません。そのため、2通りある解法のどちらも、最初に「片方の文字を消す」ことが解き方の方針になります。
加減法
1つ目は加減法です。加減法は与えられた2つの式同士を足したり引いたりして解を求める方法です。例題を見ながら解き方を確認していきましょう。
例題①
次の連立方程式を解いてください。
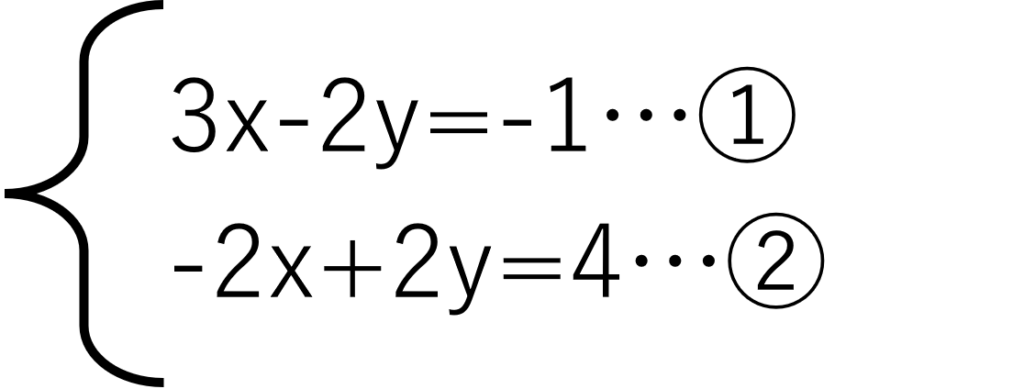
先ほど書いたように、連立方程式では文字を1つにすることが第一方針になります。
今回の式では、yに注目してみましょう。①の式には-2y、②の式には2yがあります。そのため、①+②をすることでyは消えますね。
①＋②は下のように計算できます。
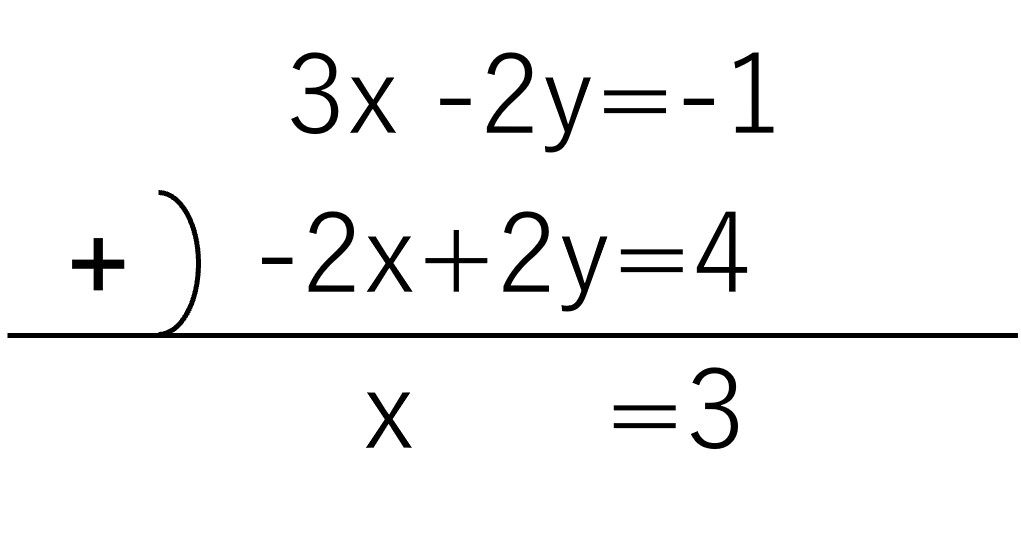
yが消え、xが求まりました。x=3だとわかったので、①の式のxに3を代入してみましょう。
すると、
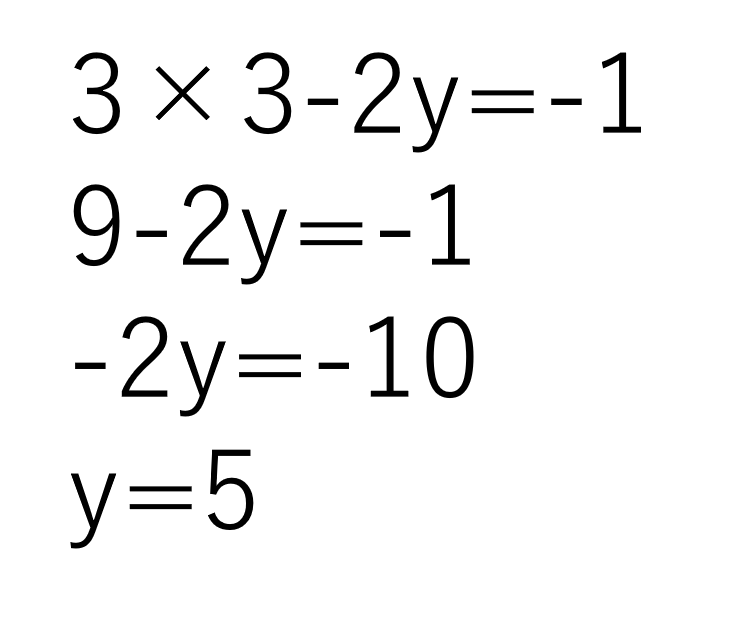
yだけの方程式になったので解けますね。解はx=3,y=5です。
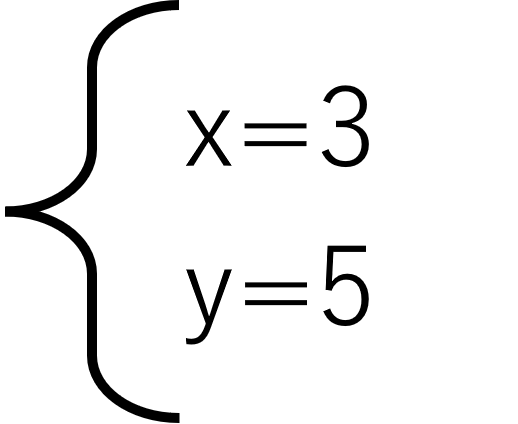や（x,y）=(3,5)など、解の書き方はいくつかありますが、学校の先生や使っている教科書の書き方に合わせるとよいでしょう。
それではもう1つ例題を解いていきましょう。次も加減法で計算します。
例題②
次の連立方程式を解いてください。
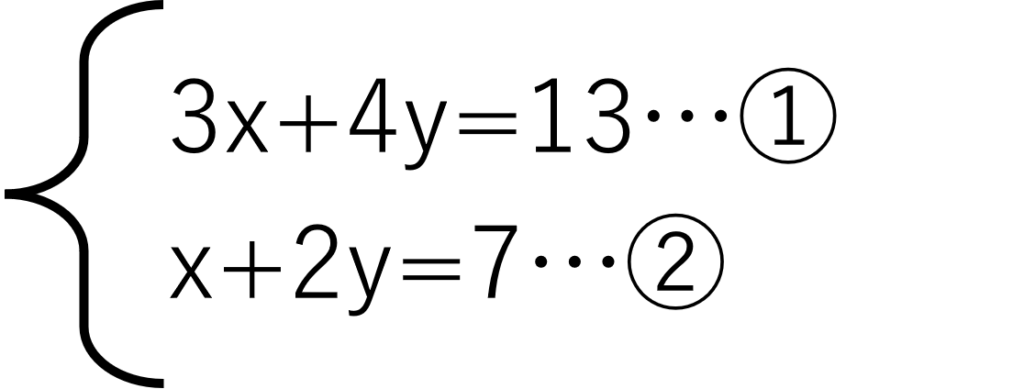
①と②の文字x,yの係数を比べてみましょう。このままでは足したり引いたりしても文字は消えませんね。
今回のように、係数が①②の式で異なるときは、係数を合わせるための計算が必要になります。この例題ではyを消す方法で計算していきます。
yの係数を揃えるため、②の式に2をかけます。
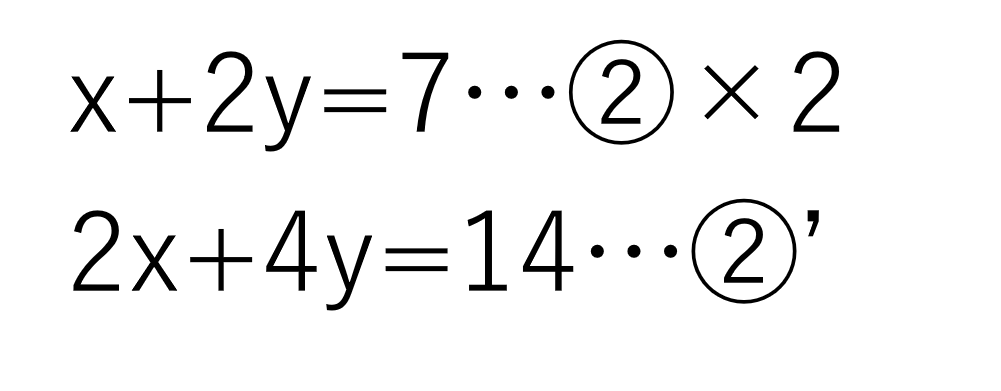
式全体に2をかけるため、x,yの係数、右辺の数もすべて2をかけてください。できた式を②'とします。
これでyの係数がそろいました。
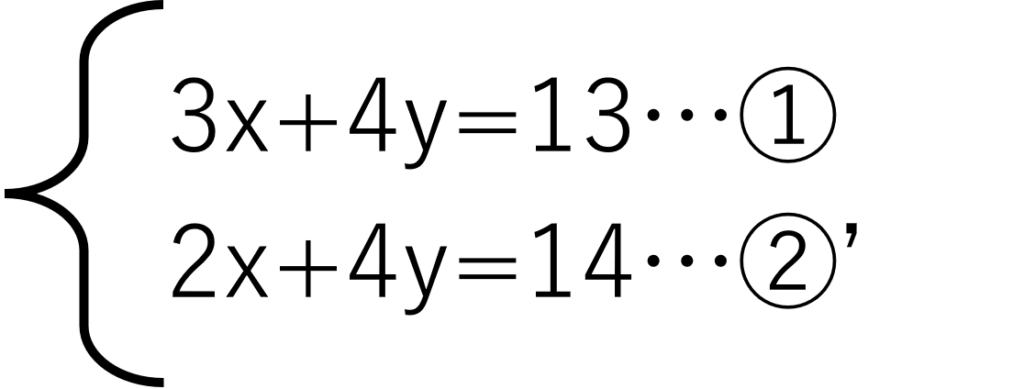
それでは①と②'は足し算すべきでしょうか？引き算すべきでしょうか？
答えは引き算です。足し算をしてしまうと、yが消えず、8yとなってしまいます。yを消すためには引き算が必要ですね。
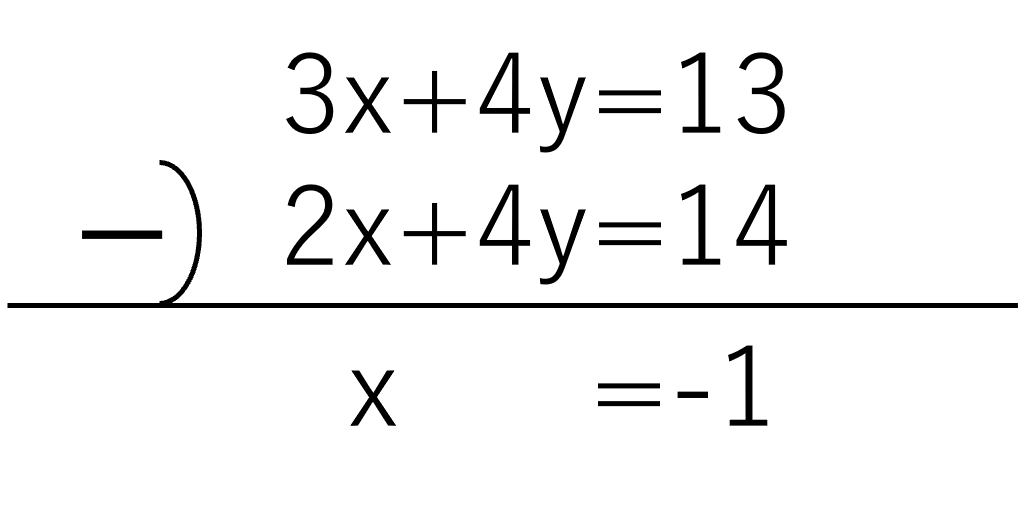
xが求まりました。①の式にx=-1を代入しましょう。
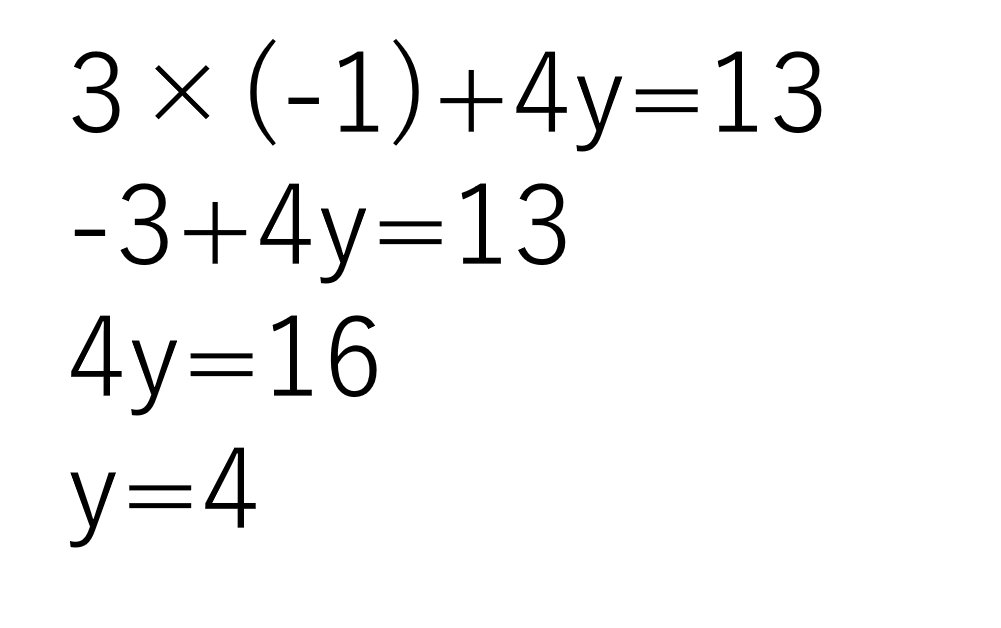
yだけの式を解くと、y=4と答えが出ました。よって解は x=-1,y=4 です。
加減法のポイント
加減法は式同士の足し引きをすることで、文字を消す方法です。
- 連立方程式の文字の係数を比較し、x,yどちらかの係数を揃える。
- 2つの式を足す（もしくは引く）
- できた一次方程式を解く
- 出てきた解を使ってもう一方の文字の値を求める。
代入法
連立方程式の解き方2つ目は、代入法です。代入法は1つの文字についての式を作り、それをもう一方の式に代入することで1つの文字を消す方法です。さっそく例題で解き方を確認していきましょう。
例題③
次の連立方程式を解いてください。
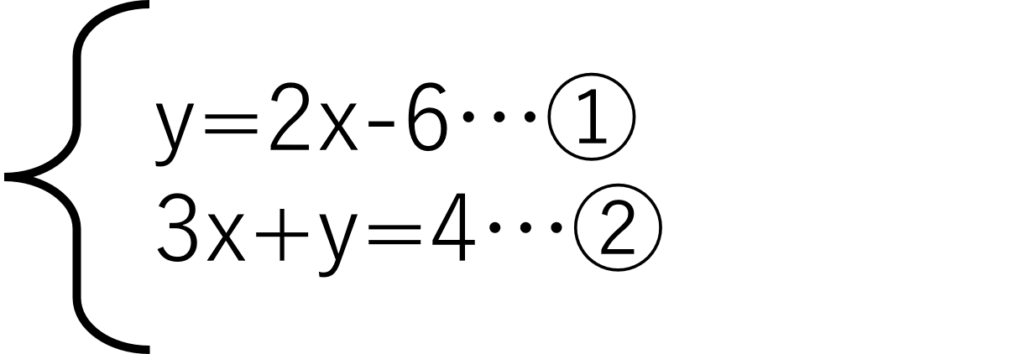
この例で注目するのは、①がy=○○の式であることです。代入法では、いずれかの文字をもう一つの文字の式で表すことが必要です。そのため、この例題のようにy=やx=の式になっていると代入法が使いやすくなります。
①の式を②に代入してみるとこのように計算できます。
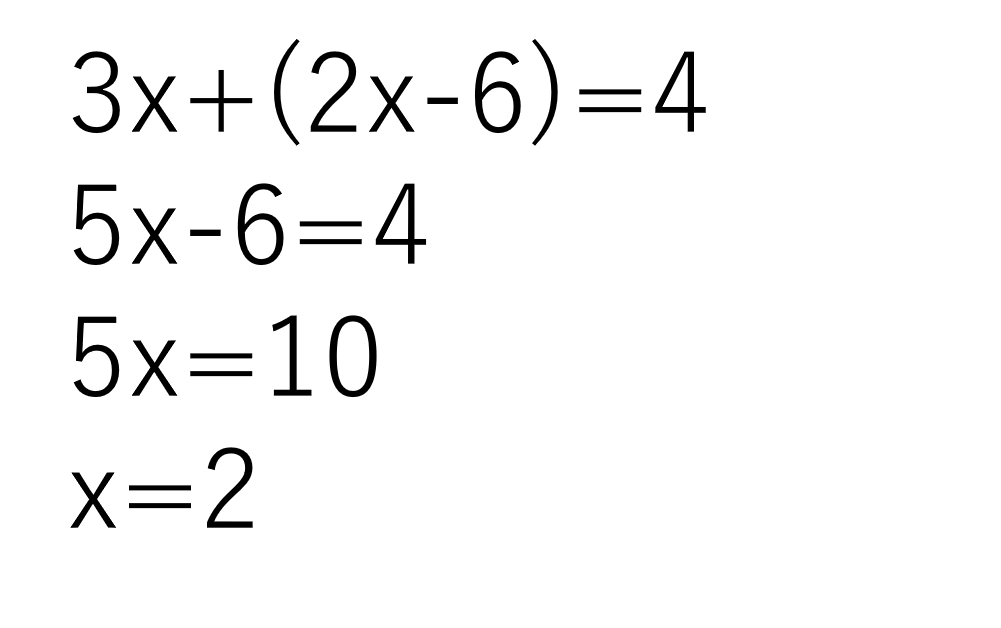
yに代入したことで、文字がxだけになり、xの値を求めることができました。最後に①の式にx=2を代入してyを求めましょう。
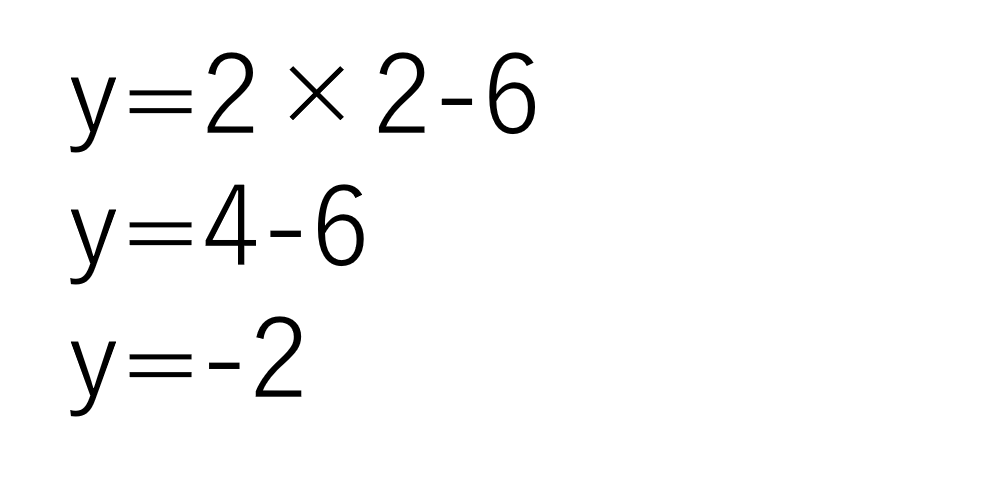
よってx=2,y=-2が解となります。
代入法のポイント
代入法は1つの文字をもう1つの文字であらわした式を代入する方法です。
- x=,もしくはy=の式を見つける（または移項して作る）。
- 1の式をもう1つの式の文字に代入する。
- 2の式を解き、1つの文字の値を求める。
- 出てきた解を使ってもう一方の文字の値を求める。
連立方程式のポイント
加減法と代入法どっちを使うべき？
ここまで基本的な連立方程式の解き方をご紹介してきました。
ここで、1つ疑問に思った人もいるかもしれません。2つの解法、どちらを使った方が良いの？という疑問です。
自分が早く、効率的に解ける方法を使うのがベストですが、一般的には加減法を使う場合が多いです。代入法の例題で扱ったような、y=,x=の式がある場合は、わざわざ移項すると時間もかかるので代入法を使うのが良いでしょう。
どちらを使うか迷ったときは、y=,x=の形があるときは代入法、それ以外は加減法で解けないかを考えてみてくださいね。
連立方程式の正答率を上げるには？
やや複雑な連立方程式、合っているか心配になるときは少なくないはず。でも合っているかどうかはテストのときに自分でも確認できます。求めた解を２つの式にあてはめて検算する習慣をつけておきましょう。片方は成り立つのにもう片方は成り立たない、そんなときは計算をし直します。この習慣で正答率をあげましょう！
連立方程式の文章題の解き方
連立方程式が解けるようになったら、次は文章題を解けるようにしていきたいですよね。一次方程式の時は求める数をxと置いて式を作りました。連立方程式の場合は、求める数が2つになりますが、式の作り方の基本は変わりません。
実際に例題を見ながら解き方を確認していきましょう。
例題
1つ120円のお菓子Aと1つ270円のお菓子Bを合わせて20個買ったところ、合計で3600円でした。お菓子A、お菓子Bをそれぞれ何個買ったか求めてください。
文章題では、まず最初にわからない数をx,yで表します。今回の場合はお菓子Aとお菓子Bの個数が分からないのでそれぞれx個、y個と表します。次に、文字を使って文章の中に出てきた数を表し、式を作っていきます。ですが、この式を作るところが難しいと感じる人も多いのではないでしょうか。特に文章が複雑になると式にするのが難しい場合も多いです。
そんな時は図や表に文章の内容をまとめるのがおすすめです。今回の場合は下のようにまとめてみましょう。
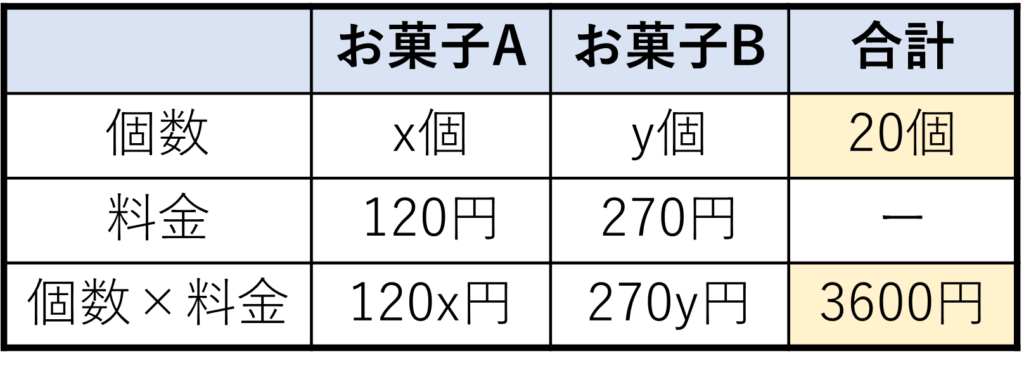
文章題からわかっているのはお菓子を合計で20個買ったら3600円だったということ。そのため、最初に20個と3600円を記入します。
そこから20個と3600円をどうやったら文字で表せるかを考えていきます。
お菓子Aはx個、お菓子Bはy個買ったので、これらを足せば20個になるはずです。つまり、x+y=20 です。
次に、120円のお菓子をx個、270円のお菓子をy個買ったのですから、料金は 120x+270y=3600 となります。
こうやってできた式2つを連立させれば問題を解くことができます。
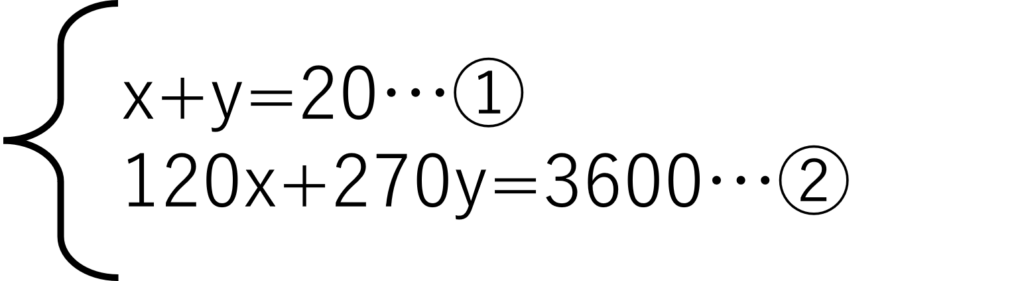
好きな方法で解いてみてくださいね。
答えは＋ボタンをタップして確認してみてください。
文章を見てパッと式を作れるようになるまでは、表や図を使って文章の中身を整理して自分なりにわかりやすくすると式の立て方が分かってきます。いろいろな種類の文章題がありますので、たくさんの問題に触れて、解いて、慣れていきましょう。
【実践問題】連立方程式の文章題を解いてみよう
【問題】
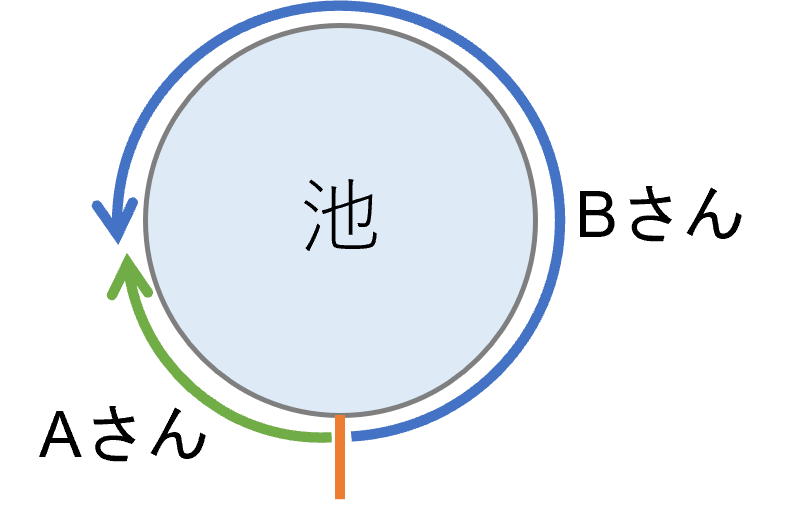
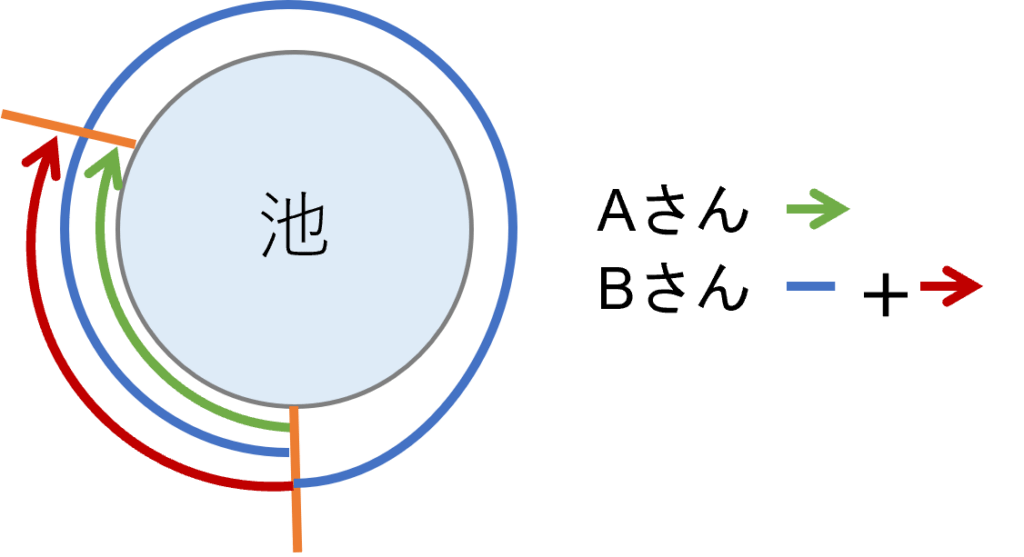
AさんとBさんが1周3kmの池の周りをまわります。
二人がスタート地点から反対方向に進むと、10分後に二人は出会います。二人がスタート地点から同じ方向に進むと、15分後にBさんが1周差をつけてAさんに追いつきます。二人の速さを求めてください。
連立方程式は文章題まで完璧に！
お困りの際は栄光ゼミナールへ
連立方程式は計算はもちろん、文章題を解けるようになることが大切です。ミスなく計算できるように整数以外の連立方程式も練習しておきましょう。
栄光の高校受験対策では都道府県によって異なる高校入試の制度や出題傾向、最新の受験情報をもとに、進路指導を行ったうえで目標達成に必要な学習プランを作成し、苦手対策、定期テスト対策、志望校対策も、講師が生徒1人ひとりに寄り添って指導します。少人数で発言や質問がしやすく、仲間と切磋琢磨しながら成長できるグループ指導と、先生と隣り合わせでわからないところや苦手を中心に、自分のペースで学習を進められる個別指導があります。自分に合った指導形態で合格に向かって効率よく学習を進めることができます。家庭学習指導にも力を入れており、志望校合格に必要な学習内容をご提案。また、模試の結果を細かく分析したうえで苦手分野を徹底的に対策することで成績向上につなげます。
はじめての方はご希望の教科を
無料で体験できます
※一部対象外のコースがございます。詳しくはお問い合わせください。
全教室の資料をメールで即お届け！
今すぐご検討いただけます。
※ご希望のすべての教室の資料が見られるURLを、メールでお送りいたします。
カンタン30秒！学び方診断
毎月LINE公式アカウントで配信
